Need help…Read on. Craving more Sumoku? Find puzzles HERE.
Weʼve had tons of requests for help in getting started on Sumoku puzzles. There really are a wide variety of strategies for these challenging puzzles, and we thought the best way to describe some of those strategies was to actually work through a puzzle from start to finish. As we solve, it might be handy for you to fill numbers into the current diagram in pencil.
Printable pdfs
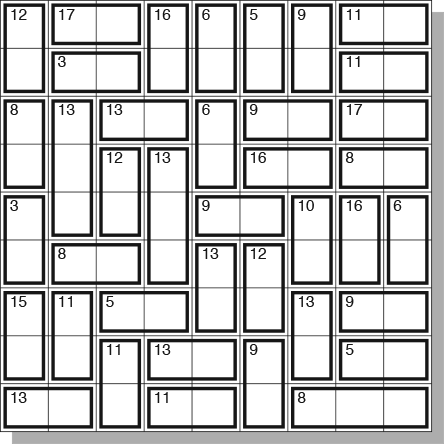 The first thing to think about are the ways that numbers can be partitioned as the sum of two other numbers. For example, on one extreme, a sum of 3 can only be broken down one way (1+2), while at the other extreme, 10 can be partitioned four ways using the digits 1 to 9 (1+9, 2+8, 3+7, and 4+6). People who solve many Sumoku puzzles become very familiar with the various combinations. Hereʼs a list:
The first thing to think about are the ways that numbers can be partitioned as the sum of two other numbers. For example, on one extreme, a sum of 3 can only be broken down one way (1+2), while at the other extreme, 10 can be partitioned four ways using the digits 1 to 9 (1+9, 2+8, 3+7, and 4+6). People who solve many Sumoku puzzles become very familiar with the various combinations. Hereʼs a list:
3 = 1+2
4 = 1+3
5 = 1+4, 2+3
6 = 1+5, 2+4
7 = 1+6, 2+5, 3+4
8 = 1+7, 2+6, 3+5
9 = 1+8, 2+7, 3+6, 4+5
10 = 1+9, 2+8, 3+7, 4+6
17 = 8+9
16 = 7+9
15 = 6+9, 7+8
14 = 5+9, 6+8
13 = 4+9, 5+8, 6+7
12 = 3+9, 4+8, 5+7
11 = 2+9, 3+8, 4+7, 5+6
 In this second diagram, Iʼve “penciled in” all pairs that can only go one way. Notice that we havenʼt quite determined the final numbers that go in the slots, but weʼve narrowed each down to just two numbers. Look at the 8|9 pair in the first row. Since no digit appears more than once in a row or column, no other slot in the first row can be an 8 or a 9. Thus, we know that the fourth slot of the first row is a 7 rather than a 9, and the fourth slot of the second row is a 9. If you look in the eighth column, you can likewise see that the third slot down in the eighth column is an 8 rather than a 9, and its partner at the end of the third row is a 9. Staying in the third row, letʼs consider how we can get a sum of 13. Itʼs not 4 and 9 or 5 and 8, since 8 and 9 are already taken, so it has to be 6 and 7. Since we already have a 7 in the fourth column, the third number of the fourth column is a 6, and its partner in the third column is a 7. We now have 6 through 9 determined for the third row. By elimination on possible partitions of 9, the sixth and seventh number in the third row are 4 and 5, in some order. The first slot in the third row isn’t 1 or 2, since 1 and 2 are already in its column. By elimination, that slot holds a 3. Its partner in the first column is a 5. Look at the 12-box in the first column. It canʼt hold 3 and 9 or 5 and 7, since 3 and 5 are taken, so it holds 4 and 8. The top number isn’t an 8 (see above), so itʼs a 4 and its partner is the 8.
In this second diagram, Iʼve “penciled in” all pairs that can only go one way. Notice that we havenʼt quite determined the final numbers that go in the slots, but weʼve narrowed each down to just two numbers. Look at the 8|9 pair in the first row. Since no digit appears more than once in a row or column, no other slot in the first row can be an 8 or a 9. Thus, we know that the fourth slot of the first row is a 7 rather than a 9, and the fourth slot of the second row is a 9. If you look in the eighth column, you can likewise see that the third slot down in the eighth column is an 8 rather than a 9, and its partner at the end of the third row is a 9. Staying in the third row, letʼs consider how we can get a sum of 13. Itʼs not 4 and 9 or 5 and 8, since 8 and 9 are already taken, so it has to be 6 and 7. Since we already have a 7 in the fourth column, the third number of the fourth column is a 6, and its partner in the third column is a 7. We now have 6 through 9 determined for the third row. By elimination on possible partitions of 9, the sixth and seventh number in the third row are 4 and 5, in some order. The first slot in the third row isn’t 1 or 2, since 1 and 2 are already in its column. By elimination, that slot holds a 3. Its partner in the first column is a 5. Look at the 12-box in the first column. It canʼt hold 3 and 9 or 5 and 7, since 3 and 5 are taken, so it holds 4 and 8. The top number isn’t an 8 (see above), so itʼs a 4 and its partner is the 8.
 The 7 in the first column isn’t in the 15-box, since 8 is already used. Thus, 7 is in the bottom slot of that column. The second slot in the bottom row is a 6. The only numbers in the third row that weʼve yet to place are the 1 and 2. If the fifth slot in the third row were the 1, then number below it would be 5. Since thereʼs already a 5 in the fourth row, that canʼt be. Thus, the fifth slot in the third row is a 2, and a 4 is below it. By elimination in the third row, the second slot holds the 1. That means the second slot in the second column holds a 2, and its partner in the 3-box is a 1. Thereʼs another 6-box in the fifth column. It canʼt hold 2 and 4, so it holds 1 and 5, in some order. The 1 canʼt be in the second slot, so the 5 is, and the 1 is in the top slot.
The 7 in the first column isn’t in the 15-box, since 8 is already used. Thus, 7 is in the bottom slot of that column. The second slot in the bottom row is a 6. The only numbers in the third row that weʼve yet to place are the 1 and 2. If the fifth slot in the third row were the 1, then number below it would be 5. Since thereʼs already a 5 in the fourth row, that canʼt be. Thus, the fifth slot in the third row is a 2, and a 4 is below it. By elimination in the third row, the second slot holds the 1. That means the second slot in the second column holds a 2, and its partner in the 3-box is a 1. Thereʼs another 6-box in the fifth column. It canʼt hold 2 and 4, so it holds 1 and 5, in some order. The 1 canʼt be in the second slot, so the 5 is, and the 1 is in the top slot.
The third diagram shows our long overdo update. See if you understand how everything has been filled in.
Just for a change of pace, Iʼm going to switch solving strategies for a minute. Look at the first column. It includes all of the digits 1 to 9, so the sum of the numbers in the first column is 1+2+3+4+5+6+7+8+9 = 45. There are four vertically oriented boxes in that column; a 12-box, an 8-box, a 3-box, and a 15-box. The sum of these numbers is (12+8+3+15 =) 38. That means that the one number not in a vertical box is (45-38 =) 7. We already discovered that fact, but we could have known it right from the start. Now letʼs use the same idea to find a number we didn’t already know. Follow the thin line that separates the seventh column from the eighth column. Notice that it doesn’t cross any boxes until it gets to the last row. The complete boxes in the eighth and ninth columns have sum numbers of 11, 11, 17, 8, 16, 6, 9, and 5 for a total of 83. The only slots we havenʼt counted from the eighth and ninth columns are the last two slots in the ninth row that are part of a box with a sum of 8. Now, we know that the sum of the numbers in each column is 45, so the sum for the last two columns is 45+45 = 90. We saw that the complete boxes summed to 83, so the incomplete part must total 90-83 = 7. That is, the last two slots in the last row sum to 7. Therefore, the seventh number in the last row is 1. Wow!
Weʼre going to use the idea again in the seventh column. There are three vertical boxes there: a 9-box, a 10-box, and a 13-box. That makes 32 in those six slots. We have a 1 at the bottom, so the seven slots total 33. That leaves 45-33 = 12 for the two remaining slots. We saw before that one of them was 4 or 5 and the other was 7 or 9. The only way they add up to 12 is if the first is 5 and the second is 7. Their partners in the sixth column are 4 and 9, respectively. Weʼll do this one more time for the sixth column. The vertical boxes are marked with sums of 5, 12, and 9 for a total of 26. we have 4 and 9 in the third and fourth slots, which brings our column total to 39. Thus, the fifth slot in the column is 45-39 = 6. The fifth number in the fifth column must then be a 3. Since we already have the 4 in the sixth column, the 5-box at the top of the column must hold 2 and 3. We have the 2 in the second row, so the the bottom of the 5-box holds the 3, and the top holds the 2. Time to update the diagram.
 Things are going to move along quickly from here, and Iʼll forgo some unnecessary explanations. Since we know the 8 in the first row is in the second or third slot, the 3 in the first row isnʼt in the 11-box in that row; itʼs in the seventh slot. The number below it is a 6. The 1 in the sixth column isnʼt in the 12-box nor is it in the bottom row, so itʼs in the eighth slot. Below it is the 8. The horizontal boxes in the last row hold 13, 11, and 8 for a total of 32. The 8 in the sixth slot makes 40, so the third slot holds the 5. The number above it is the 6. The 6 in the first column must by elimination be in the seventh slot. The number below it is a 9. Since weʼve placed the 1 in the seventh column, the 9 in that column isnʼt in the 10-box, so itʼs in the seventh slot in that column. The number below it is a 4. Weʼve placed the 6 in the eighth row, so the 7 in that row isnʼt in the 13-box. Nor obviously is it in the 5-box, so the 7 is in the second slot.
Things are going to move along quickly from here, and Iʼll forgo some unnecessary explanations. Since we know the 8 in the first row is in the second or third slot, the 3 in the first row isnʼt in the 11-box in that row; itʼs in the seventh slot. The number below it is a 6. The 1 in the sixth column isnʼt in the 12-box nor is it in the bottom row, so itʼs in the eighth slot. Below it is the 8. The horizontal boxes in the last row hold 13, 11, and 8 for a total of 32. The 8 in the sixth slot makes 40, so the third slot holds the 5. The number above it is the 6. The 6 in the first column must by elimination be in the seventh slot. The number below it is a 9. Since weʼve placed the 1 in the seventh column, the 9 in that column isnʼt in the 10-box, so itʼs in the seventh slot in that column. The number below it is a 4. Weʼve placed the 6 in the eighth row, so the 7 in that row isnʼt in the 13-box. Nor obviously is it in the 5-box, so the 7 is in the second slot.  A 4 is directly above it. The 9 in the bottom row is in the fifth slot. The 2 is to its left. The 5-box in the seventh row doesnʼt hold 1 and 4; it holds 2 and 3, in some order. That 2 isnʼt in the fourth column; itʼs in the third, and the 3 is in the fourth slot. The 6 in the fifth column is in the sixth slot. The 7 is below it. By elimination in the fifth column, the eighth slot holds an 8. Its partner is a 5. The 7 in the sixth column is, by elimination, in the sixth slot, and a 5 is below it. Thus, sixth slot of the eighth column isnʼt a 7; itʼs a 9 (see above), and thereʼs a 7 above it. The eight in the seventh row is in the last slot, and the 1 is beside it. The 8-box in the sixth row doesnʼt hold 6and 2 or 7 and 1; it holds 5 and 3. The 5 isnʼt in the third slot, so itʼs in the second, and the 3 is in the third. The 4 in the third column is, by elimination, in the fifth slot. The 8 is above it, and the 9 is at the top of the column. The second slot of the first row holds an 8 (see above). The 7 in the second row is, by elimination, in the ninth slot. A 4 is beside it. The 4 in the ninth row is in the ninth slot, and a 3 is beside it. The 3 in the eighth row is in the ninth slot, and the 2 is beside it. The 2 in the fourth row is in the ninth slot, and the 6 is beside it. The 6 in the first row is in the ninth slot, and the 5 is beside it. The 5 in the ninth column is in the fifth slot, and the 1 is below it. The first slot of the sixth row holds a 2, and thereʼs a 1 above it. The 2 in the sixth column is in the fifth slot, and the 8 is below it. The fourth slot in the sixth row is a 4. The 3 in the fourth row is in the second slot, and the 9 is below it. Finally, in the fourth column, the 1 is above the 8.
A 4 is directly above it. The 9 in the bottom row is in the fifth slot. The 2 is to its left. The 5-box in the seventh row doesnʼt hold 1 and 4; it holds 2 and 3, in some order. That 2 isnʼt in the fourth column; itʼs in the third, and the 3 is in the fourth slot. The 6 in the fifth column is in the sixth slot. The 7 is below it. By elimination in the fifth column, the eighth slot holds an 8. Its partner is a 5. The 7 in the sixth column is, by elimination, in the sixth slot, and a 5 is below it. Thus, sixth slot of the eighth column isnʼt a 7; itʼs a 9 (see above), and thereʼs a 7 above it. The eight in the seventh row is in the last slot, and the 1 is beside it. The 8-box in the sixth row doesnʼt hold 6and 2 or 7 and 1; it holds 5 and 3. The 5 isnʼt in the third slot, so itʼs in the second, and the 3 is in the third. The 4 in the third column is, by elimination, in the fifth slot. The 8 is above it, and the 9 is at the top of the column. The second slot of the first row holds an 8 (see above). The 7 in the second row is, by elimination, in the ninth slot. A 4 is beside it. The 4 in the ninth row is in the ninth slot, and a 3 is beside it. The 3 in the eighth row is in the ninth slot, and the 2 is beside it. The 2 in the fourth row is in the ninth slot, and the 6 is beside it. The 6 in the first row is in the ninth slot, and the 5 is beside it. The 5 in the ninth column is in the fifth slot, and the 1 is below it. The first slot of the sixth row holds a 2, and thereʼs a 1 above it. The 2 in the sixth column is in the fifth slot, and the 8 is below it. The fourth slot in the sixth row is a 4. The 3 in the fourth row is in the second slot, and the 9 is below it. Finally, in the fourth column, the 1 is above the 8.
By utilizing the facts and techniques developed here, and exercising a lot of patience, you can become a skilled Sumoku solver in no time.
